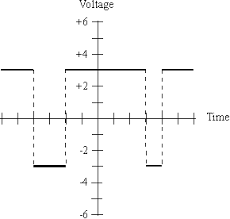
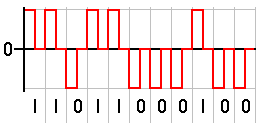
Sampling is defined as, “The process of measuring the instantaneous values of continuous-time signal in a discrete form.”

Sample is a piece of data taken from the whole data which is continuous in the time domain.

When a source generates an analog signal and if that has to be digitized, having 1s and 0s i.e., High or Low, the signal has to be discretized in time. This discretization of analog signal is called as Sampling.

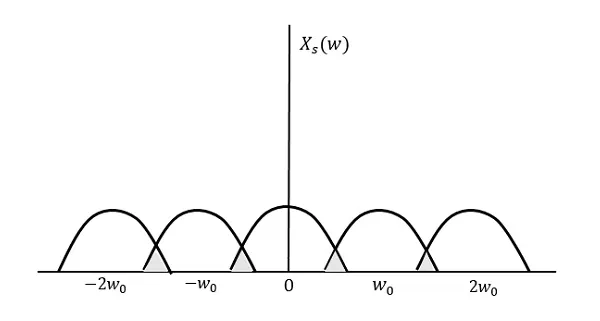
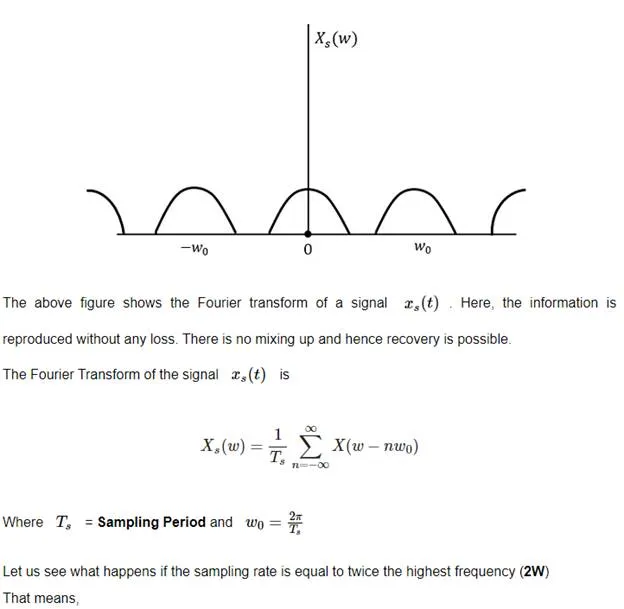
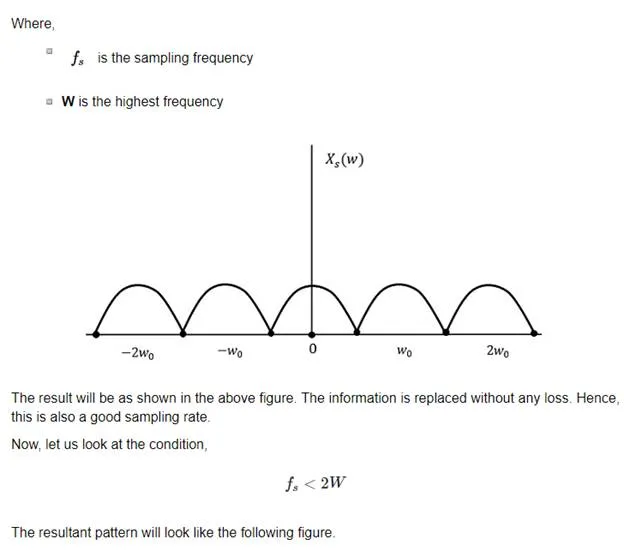
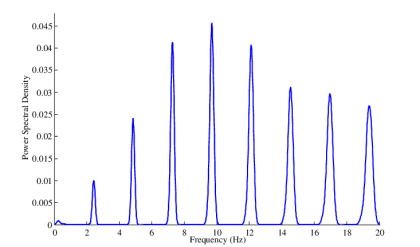
We can observe from the above pattern that the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.

Aliasing

Aliasing can be referred to as “the phenomenon of a high-frequency component in the spectrum of a signal, taking on the identity of a low-frequency component in the spectrum of its sampled version.”

The corrective measures taken to reduce the effect of Aliasing are −

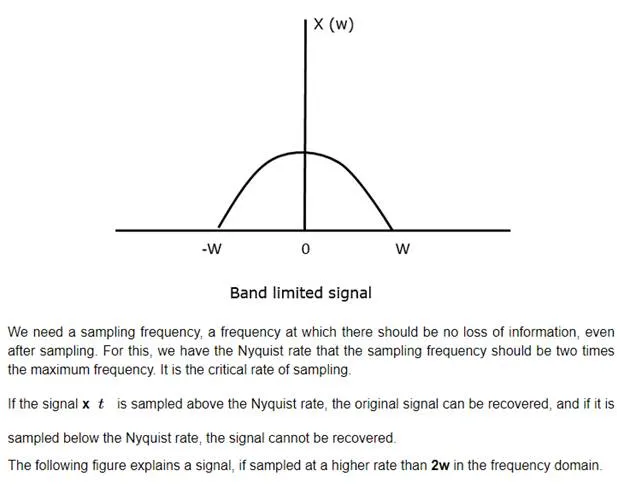
·        In the transmitter section of PCM, a low pass anti-aliasing filter is employed, before the sampler, to eliminate the high frequency components, which are unwanted.

·        The signal which is sampled after filtering, is sampled at a rate slightly higher than the Nyquist rate.

This choice of having the sampling rate higher than Nyquist rate, also helps in the easier design of the reconstruction filter at the receiver.

Scope of Fourier Transform

It is generally observed that, we seek the help of Fourier series and Fourier transforms in analyzing the signals and also in proving theorems. It is because −

·        The Fourier Transform is the extension of Fourier series for non-periodic signals.

·        Fourier transform is a powerful mathematical tool which helps to view the signals in different domains and helps to analyze the signals easily.

·        Any signal can be decomposed in terms of sum of sines and cosines using this Fourier transform.

In the next chapter, let us discuss about the concept of Quantization.