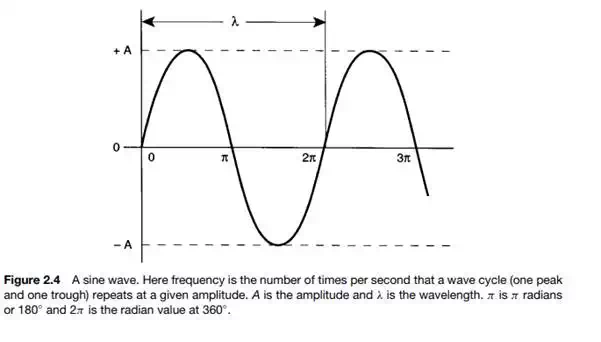
To understand more advanced telecommunication concepts, we need a firm knowledge of frequency and related parameters such as band and bandwidth, wavelength, period, and phase. Let us first define frequency and relate it to everyday life. The IEEE defines frequency as “the number of complete cycles of sinusoidal variation per unit time.” The time unit we will use is the second. For those readers with a mathematical bent, if we plot y = sin x, where x is expressed in radians, a “sine wave” is developed as shown in Figure 2.4. Figure 2.5 shows two sine waves; the left side illustrates a lower frequency, and the right side shows a higher frequency. The amplitude, measured in this case as voltage, is the excursion, up or down, at any singular point. Amplitude expresses the intensity at that point. If we spoke of amplitude without qualifying it at some point, it would be the

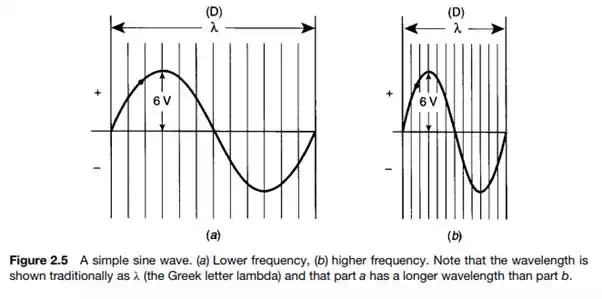
maximum excursion in the negative or positive direction (up or down). In this case it is 6 volts. If it is in the “down” direction, it would be −6 volts, based on Figure 2.5; and in the “up” direction it would be +6 volts. Frequency is an important aspect of music. For example, the key of A is 440 Hz and middle C is 263 Hz. Note that the unit of measurement of frequency used to be cycles per second (prior to 1963) and now the unit of measure is Hz named for Heinrich Hertz, a German physicist credited with the discovery of radio waves. Simple sine waves can be produced in the laboratory with a signal generator, which is an electronic oscillator that can be tuned to different frequencies. An audio signal generator can be tuned to 263 Hz, middle C, and we can hear it if the generator output is connected to a loudspeaker. These are sound frequencies. When we listen to the radio on the AM broadcast band, we may listen to a talk show on WOR, at a frequency of 710 kHz (kilohertz, meaning 710,000 Hz). On the FM band in the Phoenix, AZ, area, we may tune to a classical music station, KBAQ, at 89.5 MHz (89,500,000 Hz). These are radio frequencies.

Metric prefixes are often used, when appropriate, to express frequency as illustrated in the above paragraph. For example, kilohertz (kHz), megahertz (MHz), and gigahertz (GHz) are used for Hz × 1000, Hz × 1,000,000, and Hz × 1,000,000,000. Thus 38.71 GHz is 38.710,000,000 Hz. Wavelength is conventionally measured in meters and is represented by the symbol λ. It is defined as the distance between successive peaks or troughs of a sinusoidal wave (i.e., D in Figure 2.5). Both sound and radio waves each travel with a certain velocity of propagation. Radio waves travel at 186,000 mi/sec in a vacuum, or 3 × 108 m/sec.1 If we multiply frequency in hertz times the wavelength in meters, we get a constant, the velocity of propagation. In a vacuum (or in free space),

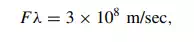
where F is measured in hertz, and λ is measured in meters (m). This is an important concept that will be freely used in the remainder of this text.